|
Se la
variazione di velocità nel tempo, vale a dire l'accelerazione, si mantiene
costante sia in modulo sia in direzione (a = costante), si
ha il moto rettilineo uniformemente accelerato o decelerato, a seconda
che la velocità aumenti o diminuisca.
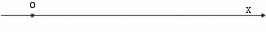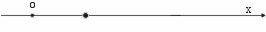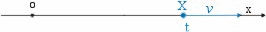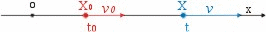
fig. 5
Con riferimento alla figura 5: ox è la
retta lungo la quale si muove il punto mobile; v0
è
la velocità del punto mobile nella posizione X0 nell'istante
t0 = 0 ; v è la velocità dello stesso punto
nella posizione X nell’istante
t. La variazione di velocità
v
-
v0 subita dal punto mobile nel passare
dalla posizione X0 alla posizione X, si realizza
nell'intervallo di tempo
t
-
t0 .
| Il
modulo dell'accelerazione sarà pertanto il rapporto: |
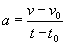 |
ovvero: |
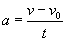 |
(1.6) |
| da cui: |
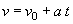 |
(1.7) |
Nel caso particolare in
cui l'istante t0 = 0 coincide con l'inizio del moto (v0
= 0),
| la
(1.7)
diventa: |
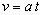 |
(1.8)
da cui |
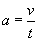 |
e |
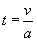 |
Dall'equazione (1.7)
ricaviamo che nel moto uniformemente accelerato, la
variazione di velocità è direttamente proporzionale al tempo in cui si
realizza.

fig. 6
Con
riferimento alla figura 6: ox è la retta lungo la
quale si muove il punto mobile;
v0
è la velocità del
punto mobile nella posizione X0
nell'istante t0;
v la velocità dello stesso punto nella posizione X
nell’istante t.
Il modulo della velocità media del punto mobile nel
passare dalla posizione X0 alla posizione X, è pari alla metà
della somma della velocità all'inizio ed alla fine dell'intervallo
considerato:
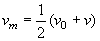 (1.9).
(1.9).
Lo spazio percorso dal punto
mobile dall'origine O alla posizione X è:
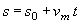 (1.10)
(1.10)
| che combinata con
la (1.9), diventa: |
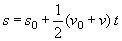 |
(1.11) |
Nel
caso particolare in cui la posizione del punto mobile nell'istante t0
coincide con il punto di riferimento O (origine del movimento), la
(1.10) diventa: 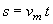 (1.12). (1.12).
| Sostituendo
nella (1.11)
il valore di v
ottenuto nella (1.7): |
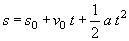 (1.13) (1.13) |
| Risolvendo la (1.7) rispetto a
t
e sostituendo nella (1.11): : |
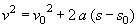 (1.14) (1.14) |
|